在数学问题中，我们经常会遇到复杂的表达式，其中包含了绝对值符号。想要解决这些问题，我们需要掌握一些绝对值化简的技巧。本文将为大家介绍一些重要的解题技巧，帮助大家轻松应对这类复杂题目。

绝对值的定义及性质

绝对值是一个常见的数学概念，表示一个数与零的距离。绝对值的定义为：对于任意实数x，其绝对值表示为|x|，它有以下性质：非负性、正定性、倒数性以及三角不等式。

绝对值的基本运算法则

绝对值有一些基本的运算法则，比如非负数的绝对值等于其本身，绝对值与加法运算的结合律等。掌握这些基本运算法则可以帮助我们更好地进行绝对值化简。

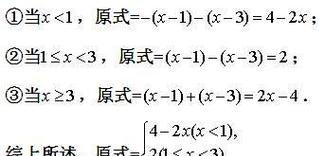
绝对值化简的常见技巧之一：分段讨论

当遇到含有绝对值的表达式时，我们可以通过分段讨论的方式来进行化简。具体来说，我们可以将表达式分为两种情况进行讨论，即x大于等于零和x小于零的情况，并根据不同情况进行相应的化简。

绝对值化简的常见技巧之二：利用绝对值的性质

绝对值有一些重要的性质，比如|x|等于x或者-x，以及|x|的平方等于x的平方。我们可以利用这些性质来进行绝对值化简，简化复杂的运算过程。

绝对值化简的常见技巧之三：利用绝对值不等式

绝对值不等式是解决含有绝对值的不等式问题时常用的工具。通过将不等式分为几个情况讨论，并利用绝对值的定义和性质，我们可以得到较为简化的不等式形式，进而解决问题。

绝对值化简的常见技巧之四：利用数轴图像

数轴图像可以直观地表示出数与零之间的距离，帮助我们更好地理解和解决含有绝对值的问题。通过画出数轴图像，我们可以更清晰地看到绝对值的取值范围，从而进行更准确的化简。

绝对值化简的常见技巧之五：利用绝对值函数的性质

绝对值函数具有一些特殊的性质，比如奇偶性和周期性。通过利用这些性质，我们可以更简化地处理含有绝对值函数的表达式，并得到更简洁的解法。

绝对值化简的常见技巧之六：巧妙运用绝对值定义

绝对值的定义是解决绝对值化简问题的基础。在一些特殊情况下，我们可以巧妙地应用绝对值的定义，从而得到简单的解法。

绝对值化简的常见技巧之七：变量替换法

对于一些复杂的绝对值表达式，我们可以通过引入一个新的变量，进行变量替换，进而简化问题。这种技巧在解决某些特殊类型的绝对值问题时非常有效。

绝对值化简的常见技巧之八：借助其他数学方法

除了以上介绍的常见技巧外，我们还可以借助其他数学方法来进行绝对值化简。比如利用因式分解、配方法等，结合绝对值的性质，可以得到更简单的解法。

绝对值化简的注意事项

在进行绝对值化简时，我们需要注意一些常见的问题。比如要注意绝对值符号的位置，避免计算错误；还需要注意化简后是否有等价性，以及化简后是否需要特殊讨论等。

绝对值化简在实际问题中的应用

绝对值化简不仅仅在数学理论中有应用，它在实际问题中也具有重要作用。比如在解决物理问题、经济问题等方面，绝对值化简可以帮助我们更好地理解和解决实际问题。

绝对值化简的练习题及解答

为了帮助读者更好地掌握绝对值化简的技巧，本文提供了一些练习题及解答。读者可以通过解题来加深对绝对值化简的理解和应用。

掌握绝对值化简，轻松应对复杂题目

通过本文的介绍，我们可以看到绝对值化简是解决复杂题目的重要技巧。掌握了这些技巧，我们能够更轻松地应对含有绝对值的表达式，从而解决数学问题。

文章结尾：通过学习和掌握绝对值化简的技巧，我们可以提高解题的效率，扩展数学思维，更好地理解和应用数学知识。希望本文能够对大家在解决绝对值问题时提供帮助，从而取得更好的成绩。